Causal Diagrams in R

Malcolm Barrett

2021-09-01

Draw your causal assumptions with causal directed acyclic graphs (DAGs)

The basic idea

  1. Specify your causal question
  2. Use domain knowledge
  3. Write variables as nodes
  4. Write causal pathways as arrows (edges)

ggdag

Step 1: Specify your DAG

library(ggdag)
dagify(
  cancer ~ smoking, 
  coffee ~ smoking
)

Step 1: Specify your DAG

dagify(
  cancer ~ smoking, 
  coffee ~ smoking 
) |> ggdag()

Step 1: Specify your DAG

Step 1: Specify your DAG

dagify(
  cancer ~ smoking + coffee, 
  coffee ~ smoking 
) |> ggdag()

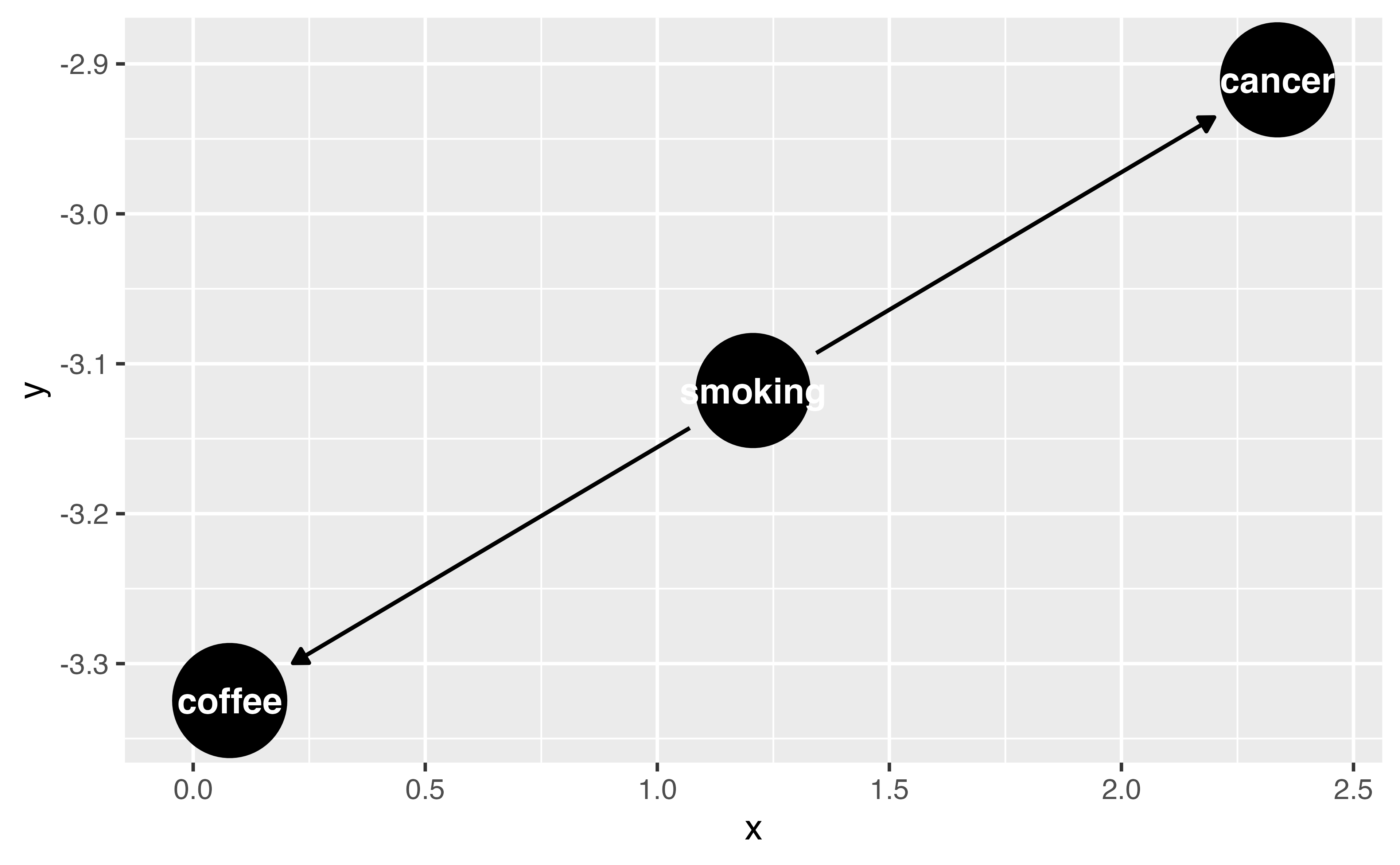
Step 1: Specify your DAG

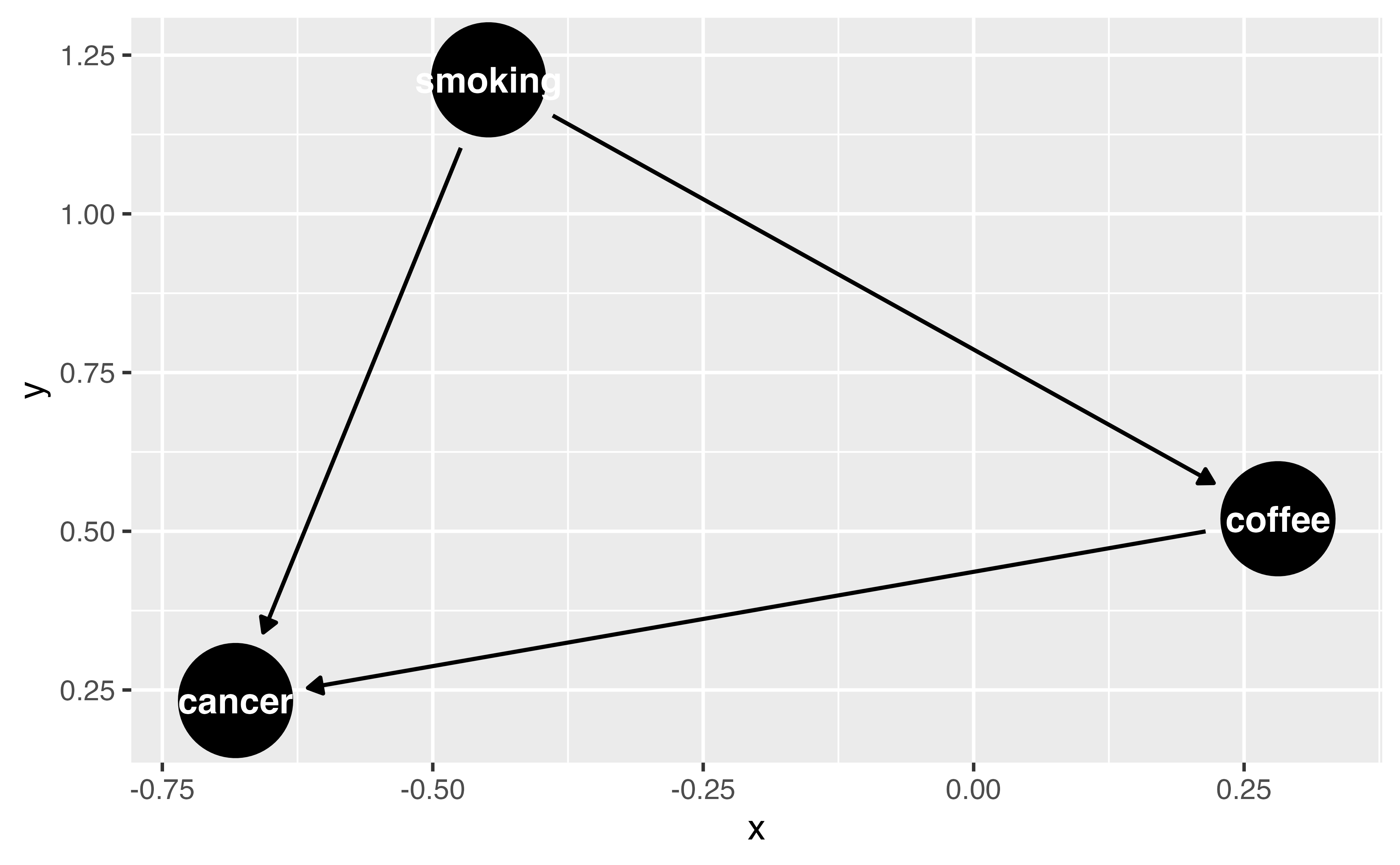
Your Turn 1 (04-dags-exercises.qmd)

Specify a DAG with dagify(). Write your assumption that smoking causes cancer as a formula.

We’re going to assume that coffee does not cause cancer, so there’s no formula for that. But we still need to declare our causal question. Specify “coffee” as the exposure and “cancer” as the outcome (both in quotations marks).

Plot the DAG using ggdag()

05:00

Your Turn 1 (02-dags-exercises.qmd)

coffee_cancer_dag <- dagify(
  cancer ~ smoking,
  smoking ~ addictive,
  coffee ~ addictive,
  exposure = "coffee",
  outcome = "cancer",
  labels = c(
    "coffee" = "Coffee", 
    "cancer" = "Lung Cancer", 
    "smoking" = "Smoking", 
    "addictive" = "Addictive \nBehavior"
  )
)
ggdag(coffee_cancer_dag)

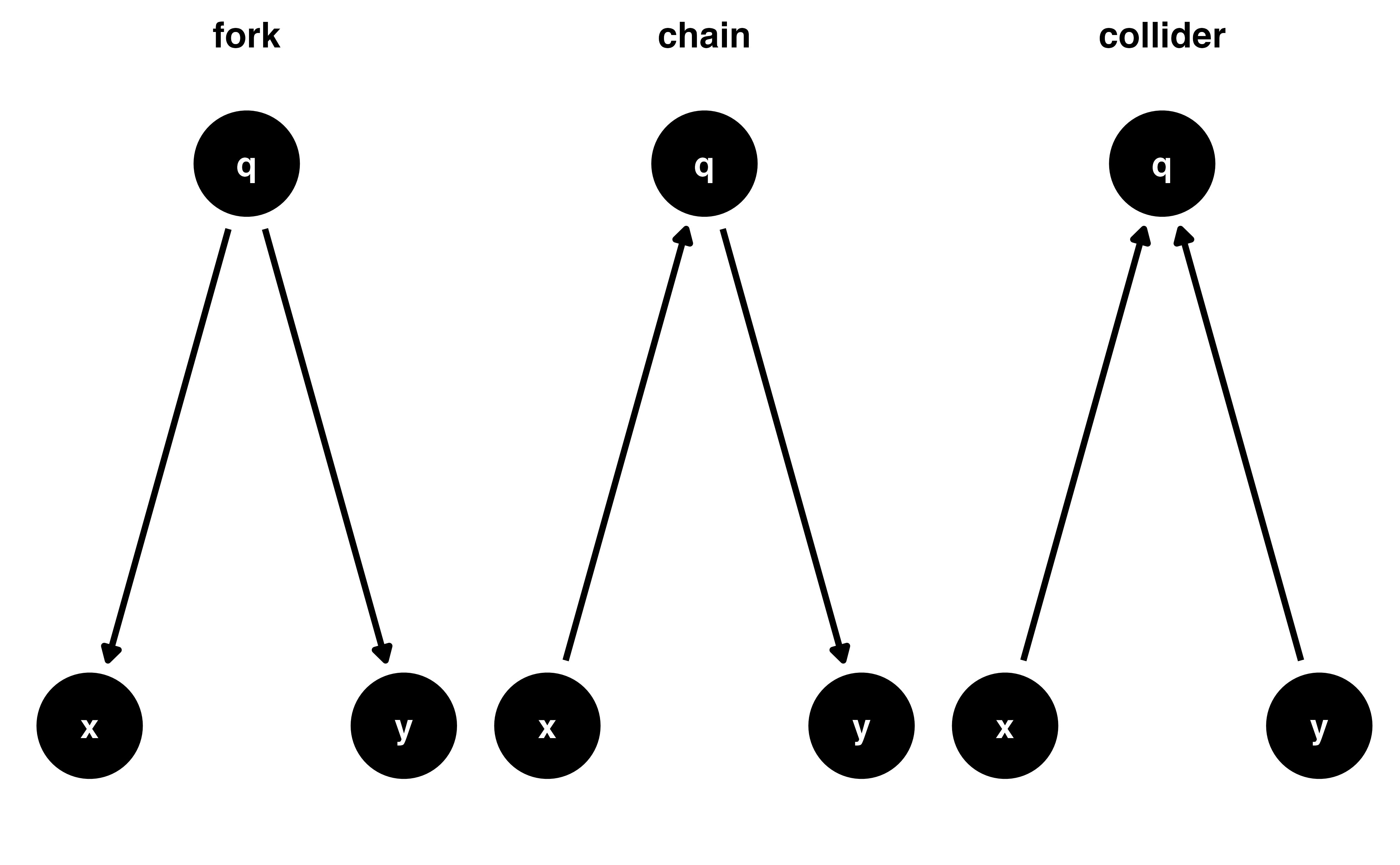
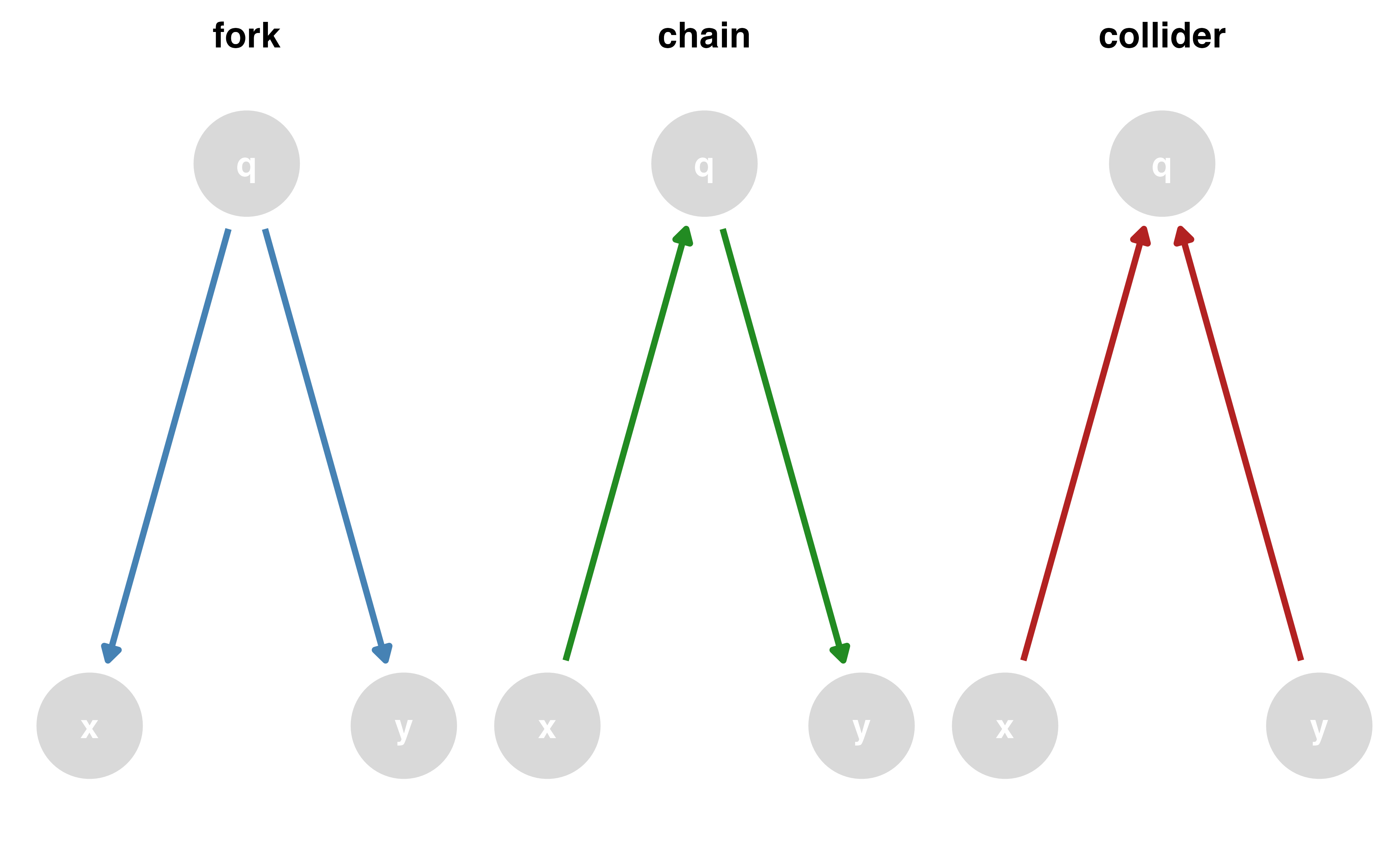
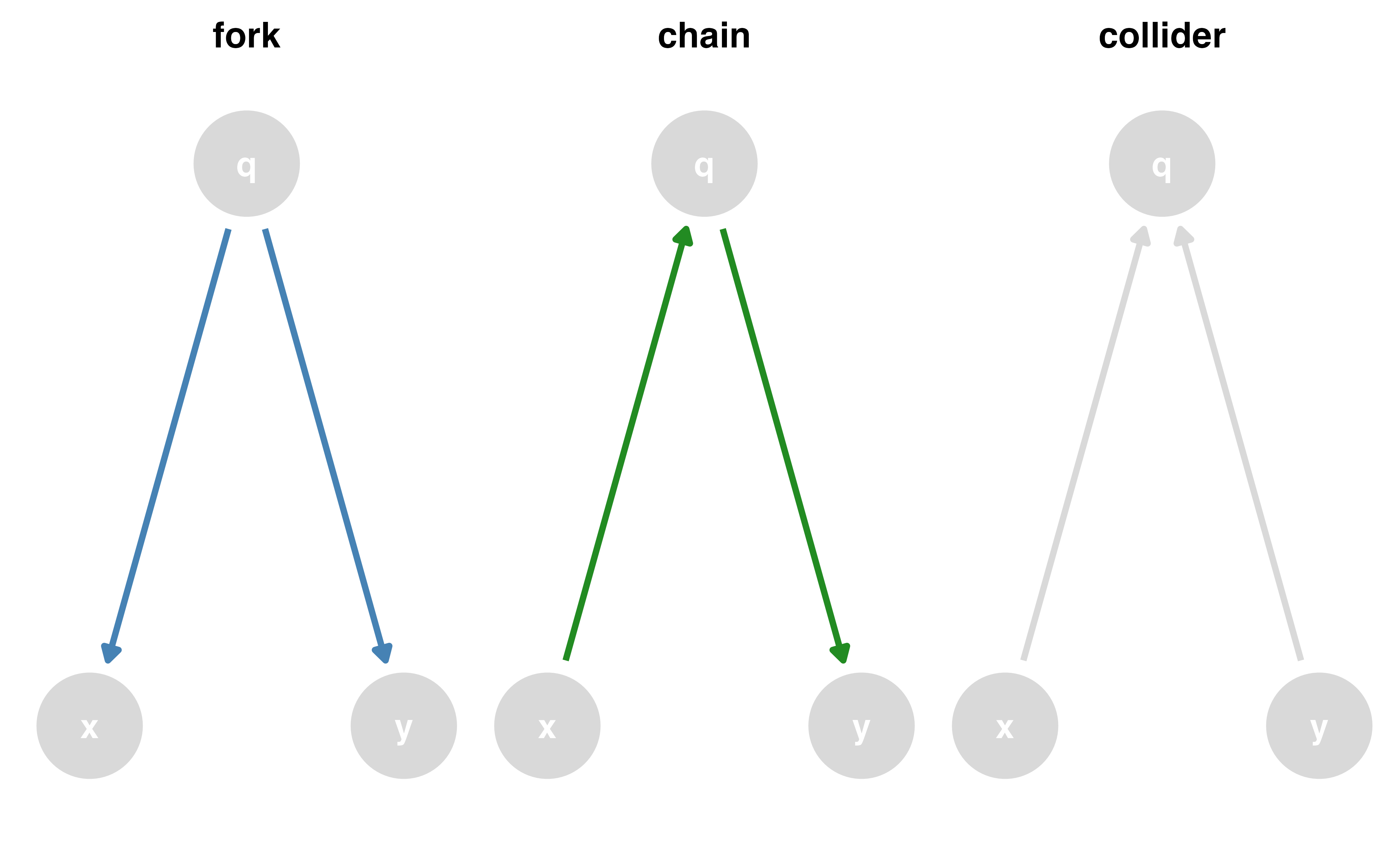
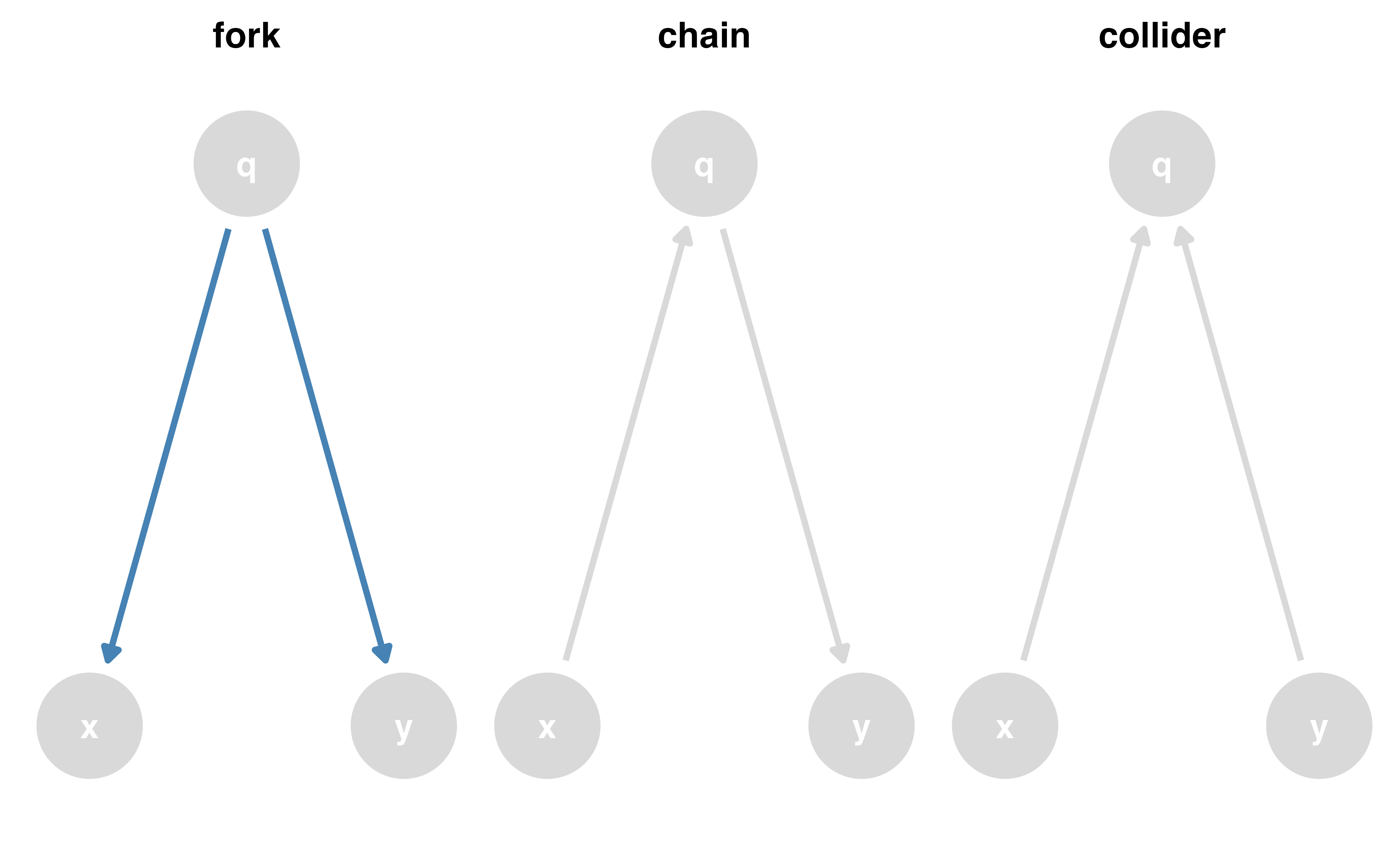
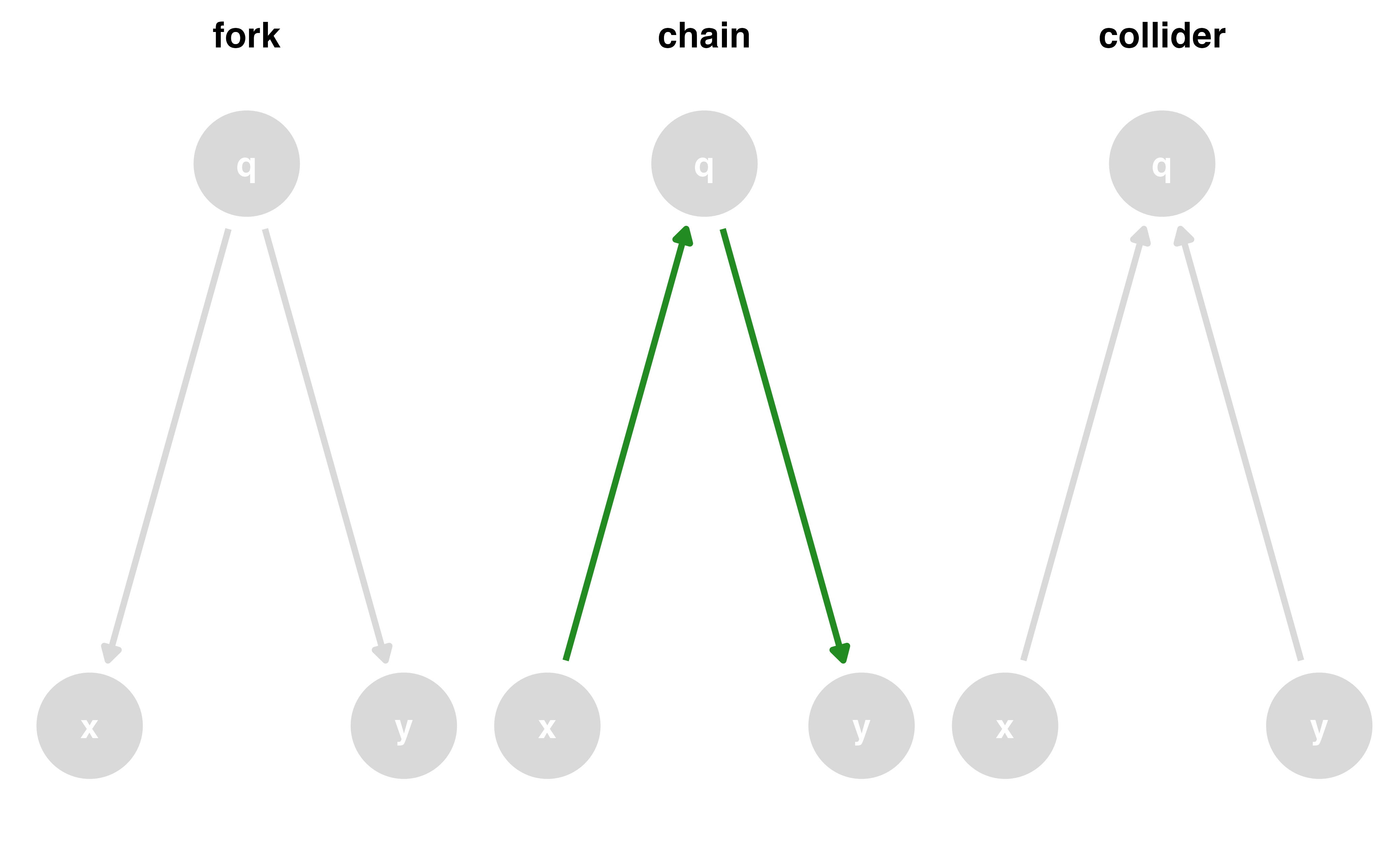
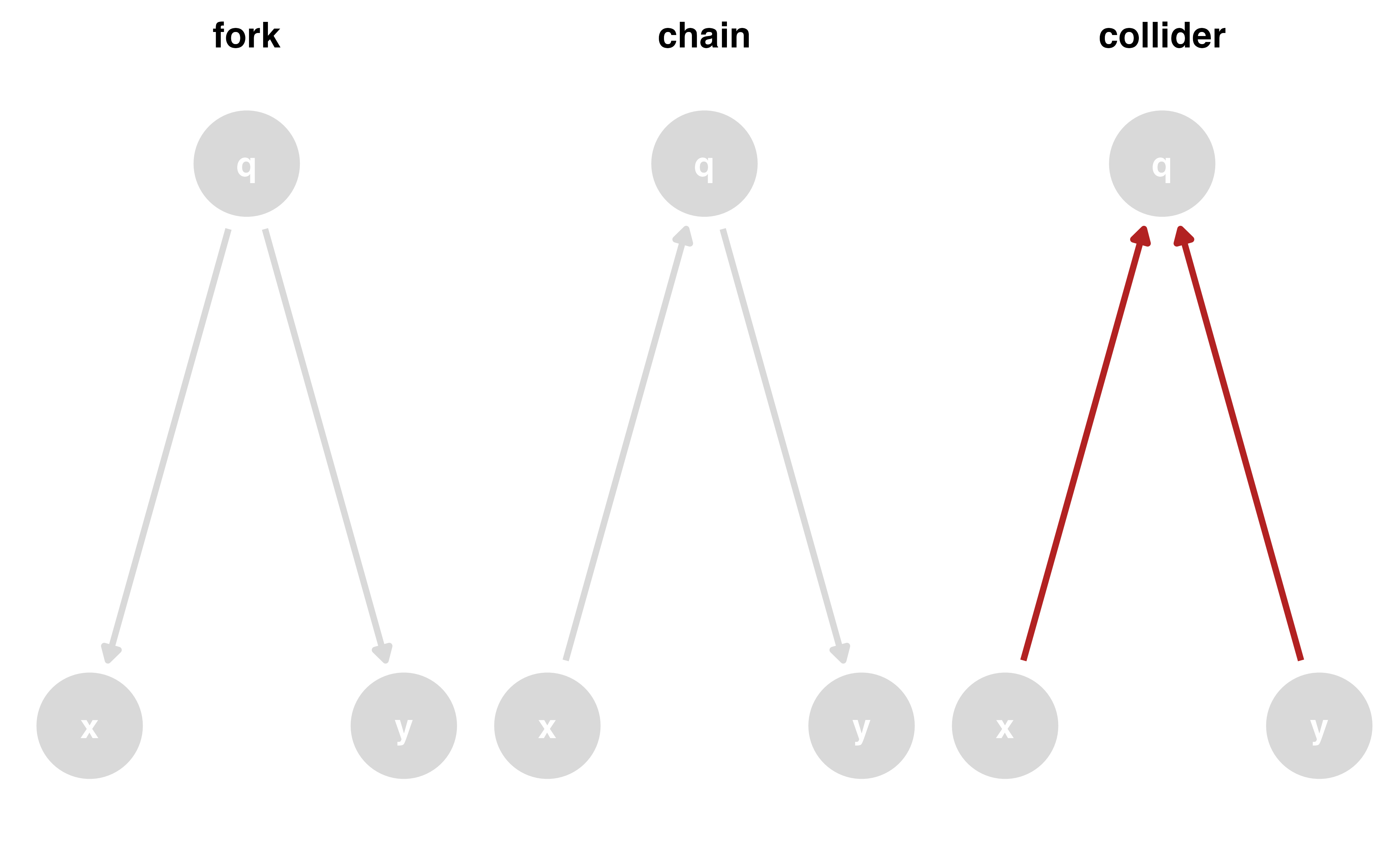
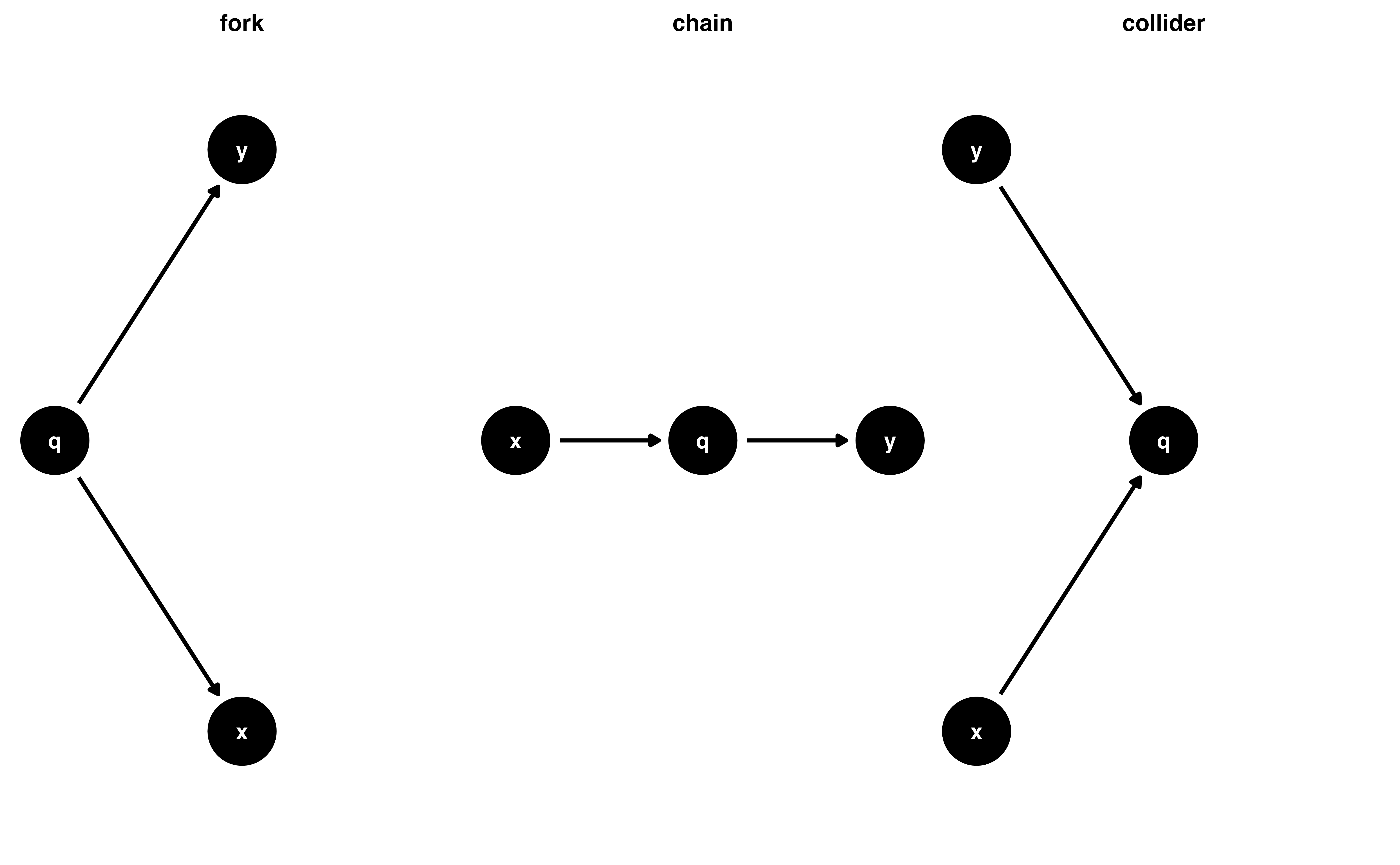
Causal effects and backdoor paths

Ok, correlation != causation. But why not?

We want to know if x -> y…

But other paths also cause associations

ggdag_paths()

Identify “backdoor” paths

ggdag_paths(smk_wt_dag)

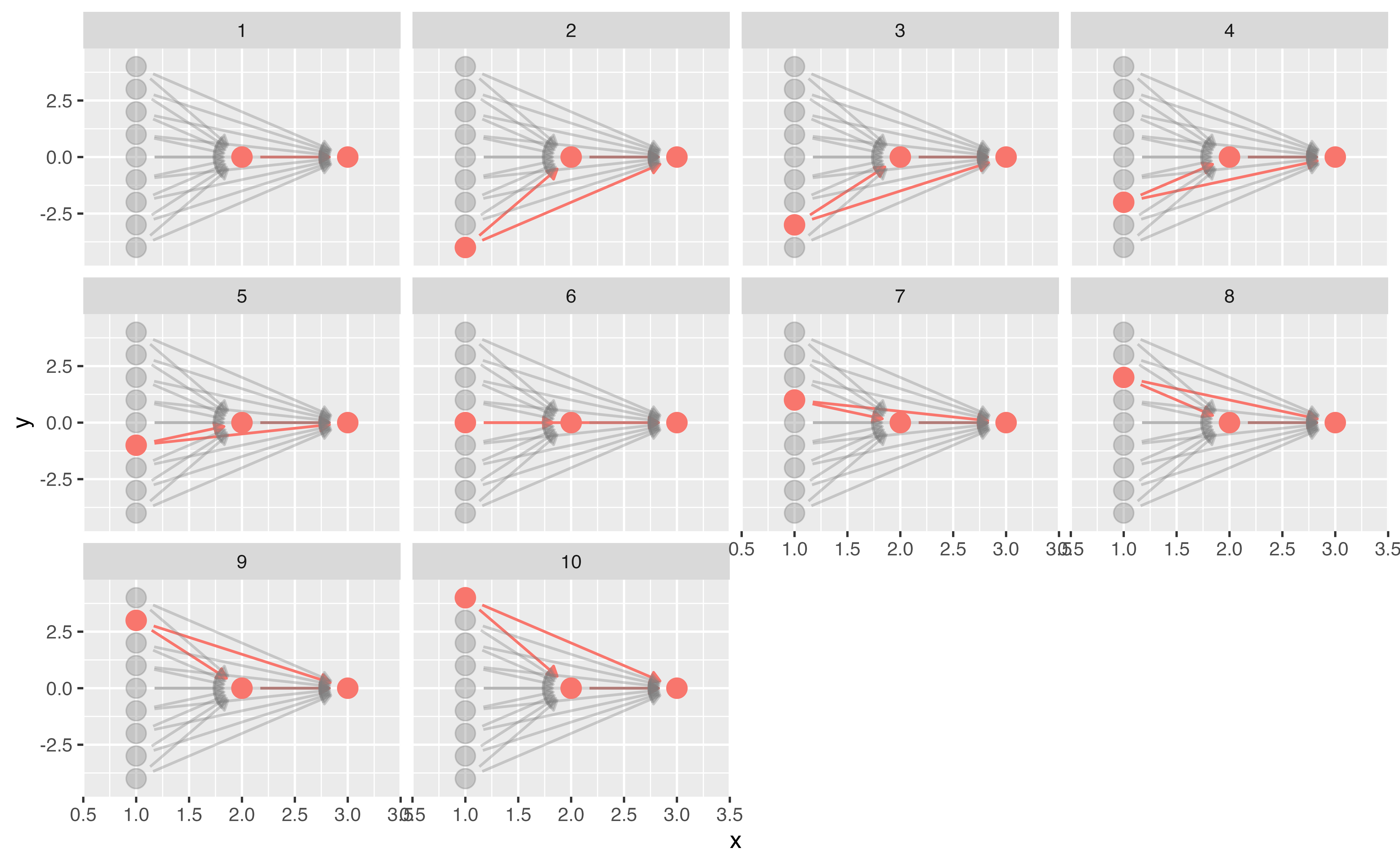
Your Turn 2

Call tidy_dagitty() on coffee_cancer_dag to create a tidy DAG, then pass the results to dag_paths(). What’s different about these data?

Plot the open paths with ggdag_paths(). (Just give it coffee_cancer_dag rather than using dag_paths(); the quick plot function will do that for you.) Remember, since we assume there is no causal path from coffee to lung cancer, any open paths must be confounding pathways.

05:00

Your Turn 2

coffee_cancer_dag |>
  tidy_dagitty() |>
  dag_paths()
# A DAG with 4 nodes and 3 edges
#
# Exposure: coffee
# Outcome: cancer
#
# A tibble: 5 × 11
  set   name          x      y direction to      xend   yend
  <chr> <chr>     <dbl>  <dbl> <fct>     <chr>  <dbl>  <dbl>
1 1     addictive 0.616 -1.27  ->        coff…  0.185 -0.127
2 1     addictive 0.616 -1.27  ->        smok…  1.09  -2.52 
3 1     cancer    1.52  -3.66  <NA>      <NA>  NA     NA    
4 1     coffee    0.185 -0.127 <NA>      <NA>  NA     NA    
5 1     smoking   1.09  -2.52  ->        canc…  1.52  -3.66 
# ℹ 3 more variables: circular <lgl>, label <chr>,
#   path <chr>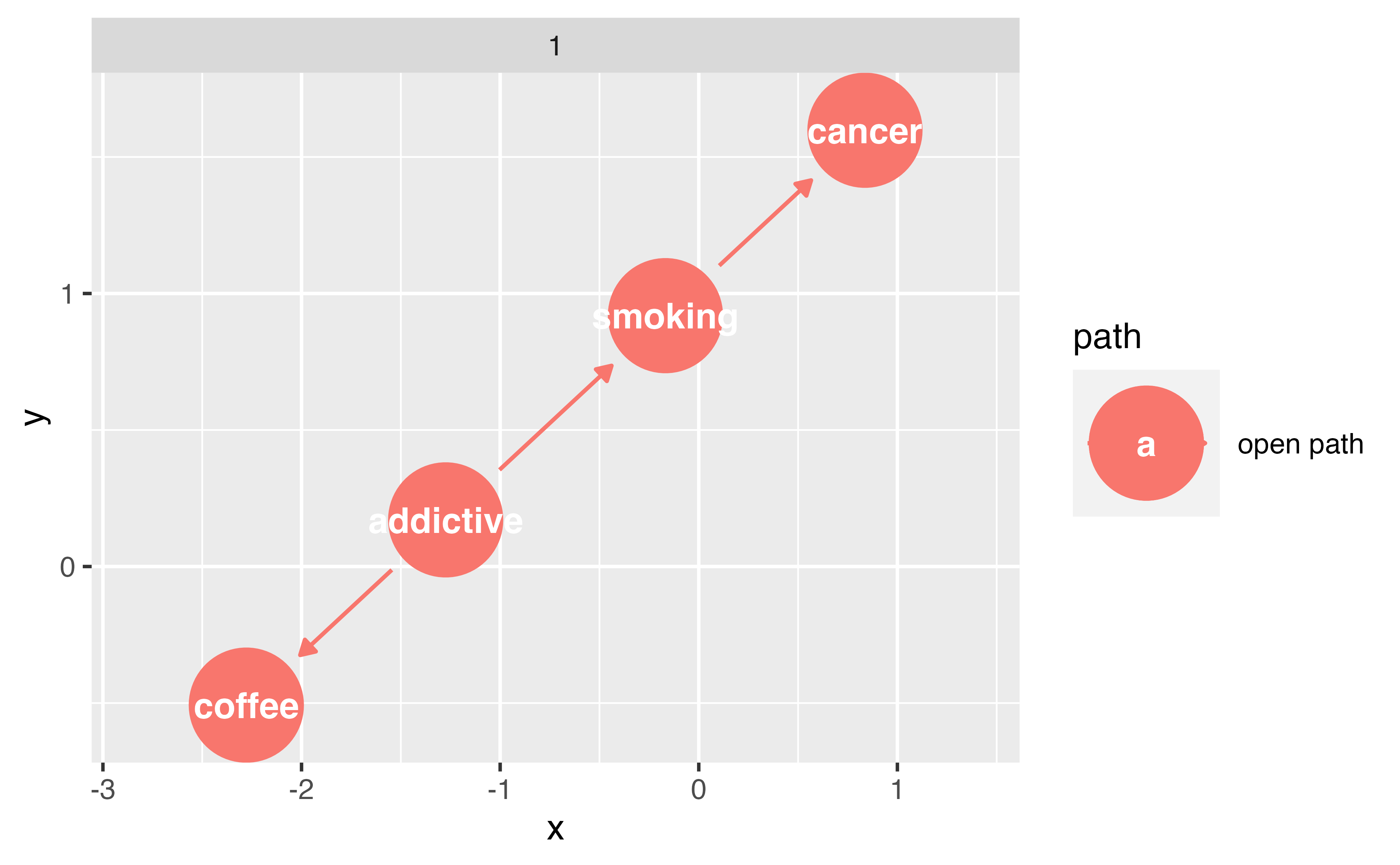
coffee_cancer_dag |>
  ggdag_paths()

Closing backdoor paths

We need to account for these open, non-causal paths

Randomization

Stratification, adjustment, weighting, matching, etc.

Identifying adjustment sets

ggdag_adjustment_set(smk_wt_dag)

Identifying adjustment sets

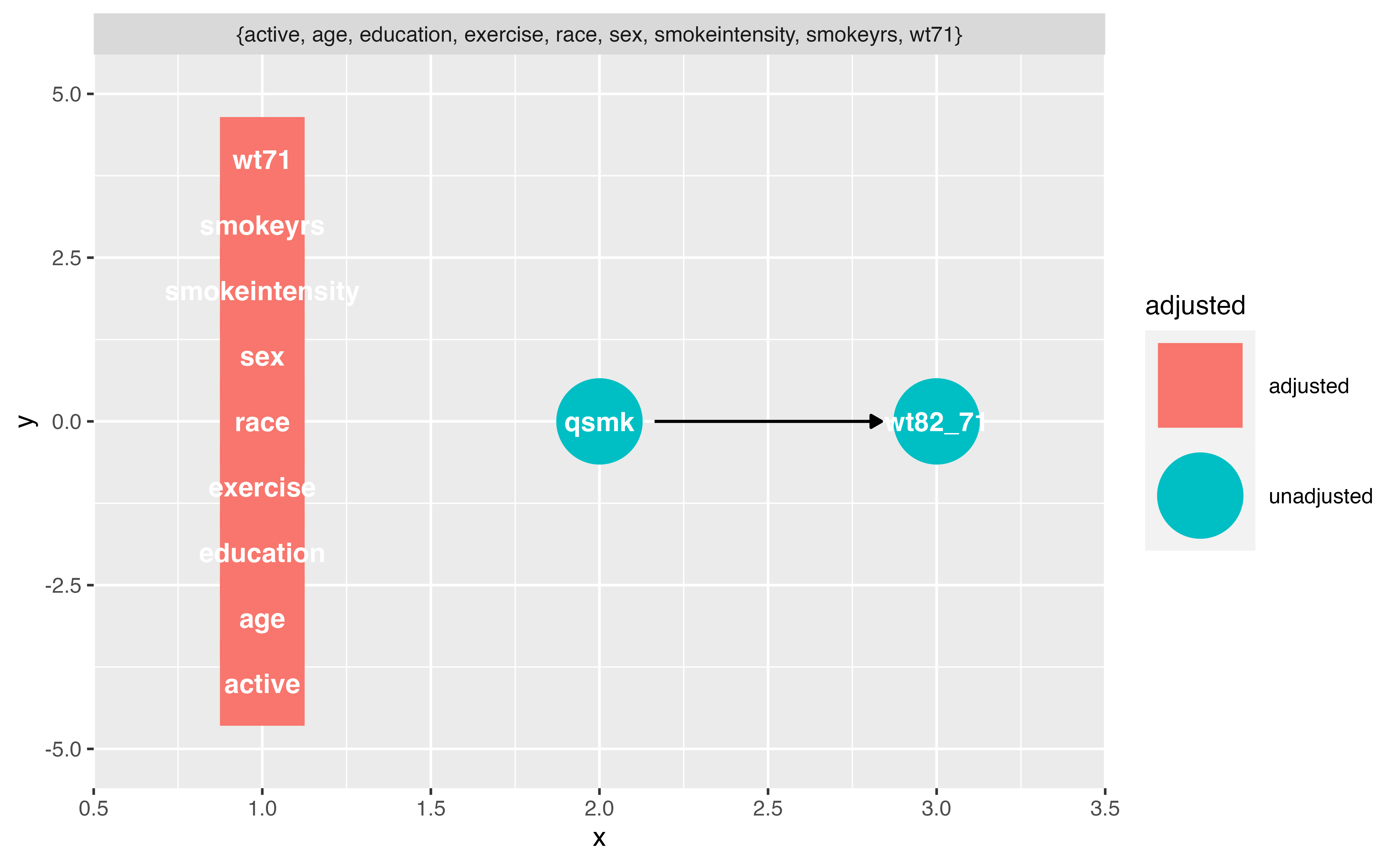
Identifying adjustment sets

library(dagitty)
adjustmentSets(smk_wt_dag)
{ active, age, education, exercise, race, sex, smokeintensity,
  smokeyrs, wt71 }

Your Turn 3

Now that we know the open, confounding pathways (sometimes called “backdoor paths”), we need to know how to close them! First, we’ll ask {ggdag} for adjustment sets, then we would need to do something in our analysis to account for at least one adjustment set (e.g. multivariable regression, weighting, or matching for the adjustment sets).

Use ggdag_adjustment_set() to visualize the adjustment sets. Add the arguments use_labels = "label" and text = FALSE.

Write an R formula for each adjustment set, as you might if you were fitting a model in lm() or glm()

05:00

Your Turn 3

ggdag_adjustment_set(
  coffee_cancer_dag, 
  use_labels = "label", 
  text = FALSE
)

Your Turn 3

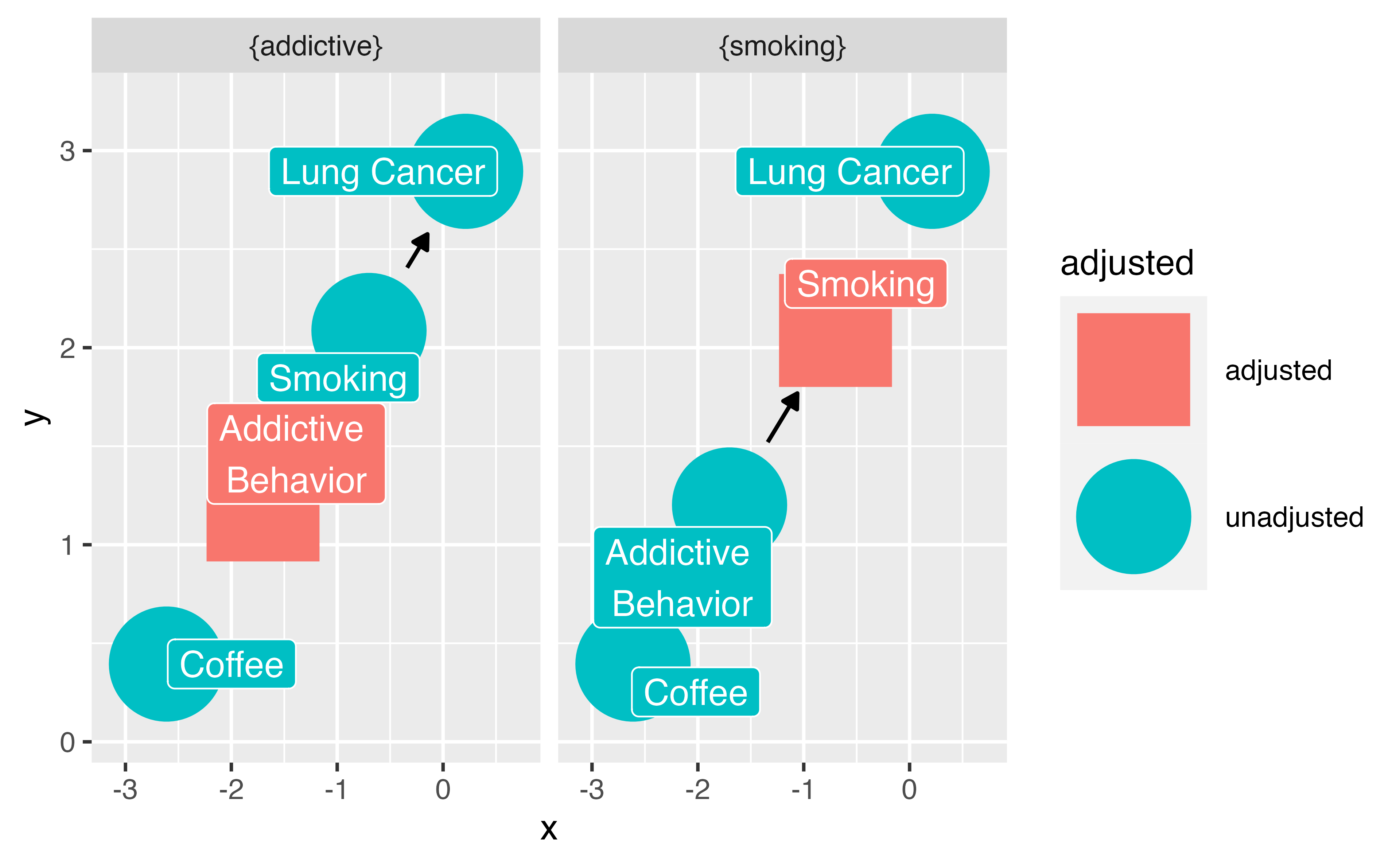
Your Turn 3

cancer ~ coffee + addictive
cancer ~ coffee + smoking

Let’s prove it!

set.seed(1234)
dag_data <- coffee_cancer_dag |> 
  simulate_data(-.6)

Let’s prove it!

dag_data
# A tibble: 500 × 4
   addictive cancer coffee smoking
       <dbl>  <dbl>  <dbl>   <dbl>
 1    0.569   3.11  -0.326  -1.29 
 2    0.411   1.52   0.330  -1.57 
 3    1.20    1.06  -0.557  -2.40 
 4   -0.782  -0.504 -0.148   0.376
 5    0.0357 -0.709 -0.342  -1.53 
 6    1.96    1.05  -1.90   -0.823
 7    1.13    0.211 -0.581  -0.534
 8    0.697   0.892 -1.36   -0.267
 9   -0.779   0.748  0.455   0.302
10   -1.13    0.930  0.568   0.742
# ℹ 490 more rows

Let’s prove it!

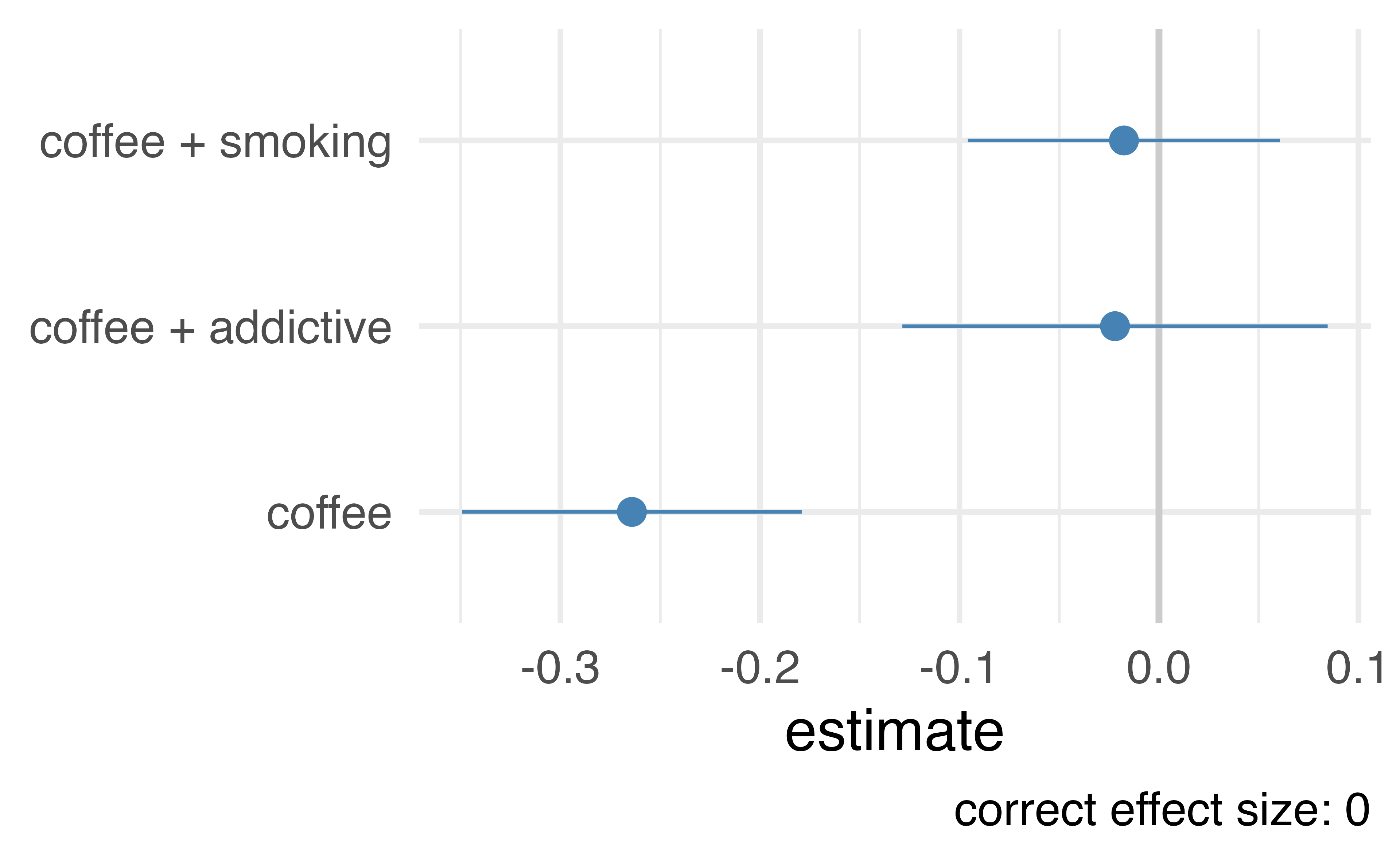
Choosing what variables to include

Adjustment sets and domain knowledge

Conduct sensitivity analysis if you don’t have something important

Common trip ups

Using prediction metrics

The 10% rule

Predictors of the outcome, predictors of the exposure

Forgetting to consider time-ordering (something has to happen before something else to cause it!)

Selection bias and colliders (more later!)

Incorrect functional form for confounders (e.g. BMI often non-linear)

Time-ordering

don’t adjust for the future!

Your Turn 4

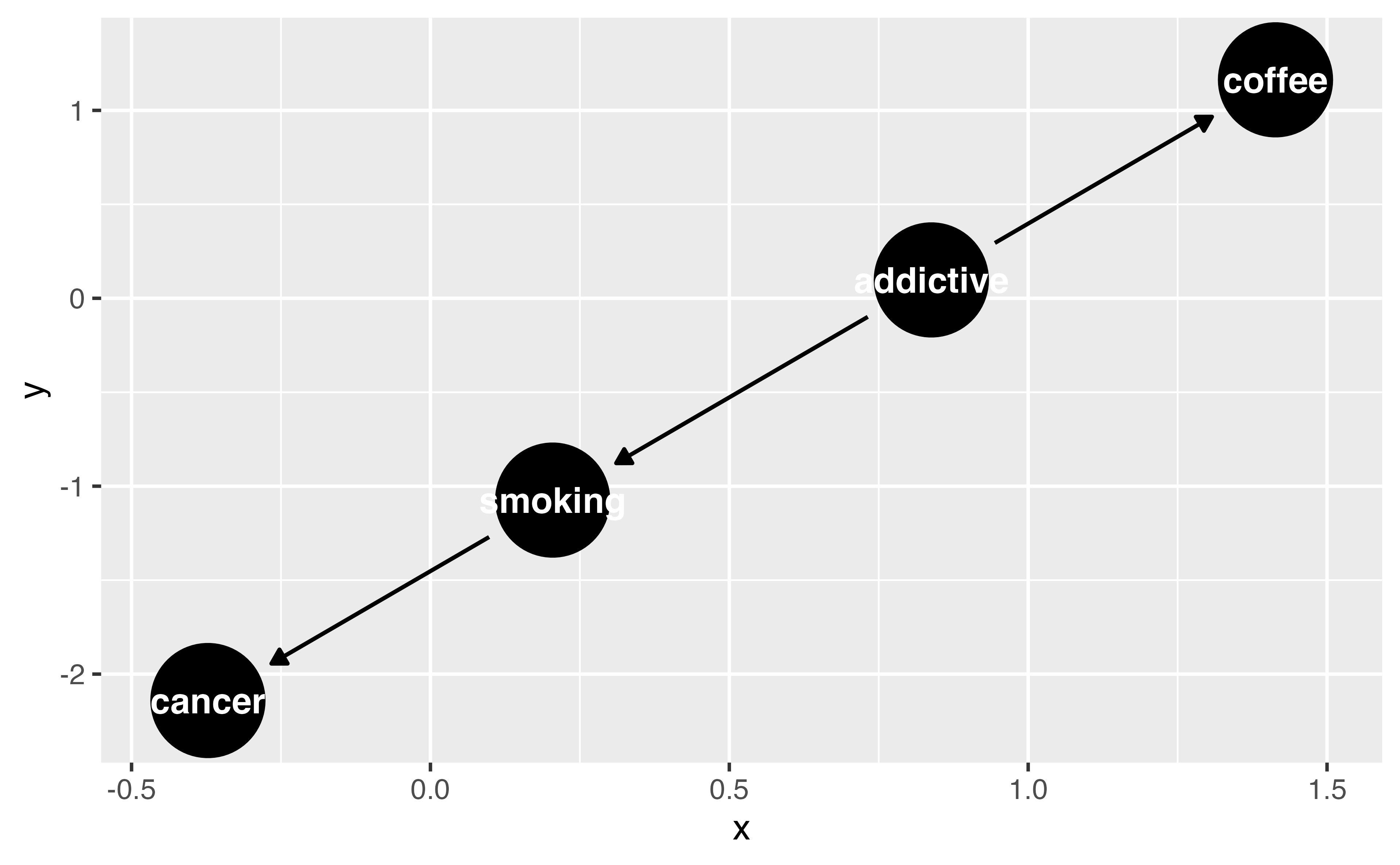
Recreate the DAG we’ve been working with using time_ordered_coords(), then visualize the DAG. You don’t need to use any arguments for this function, so coords = time_ordered_coords() will do.

Your Turn 4

coffee_cancer_dag_to <- dagify(
  cancer ~ smoking,
  smoking ~ addictive,
  coffee ~ addictive,
  exposure = "coffee",
  outcome = "cancer",
  coords = time_ordered_coords(),
  labels = c(
    "coffee" = "Coffee", 
    "cancer" = "Lung Cancer", 
    "smoking" = "Smoking", 
    "addictive" = "Addictive \nBehavior"
  )
)

#TODO: UPDATE LABELS ARGS
ggdag(coffee_cancer_dag_to, use_labels = "label", text = FALSE)

Your Turn 4

Resources: ggdag vignettes

An Introduction to ggdag

An Introduction to Directed Acyclic Graphs

Common Structures of Bias